Equazioni termodinamiche
- Categoria: Aria secca
- Pubblicato: Domenica, 27 Giugno 2010 05:02
- Scritto da Super User
- Visite: 14224
L’aria secca, per gli usi tecnologici, viene paragonata con le dovute approssimazioni ad un gas perfetto e quindi è soggetta ad una serie di equazioni e di considerazioni tipiche di un gas perfetto.
In un gas perfetto si considera che la capacità termica massica sia costante durante le varie trasformazioni termodinamiche e l’equazione che lega il volume occupato, la temperatura e la pressione è detta equazione di stato di un gas perfetto definita nei seguenti termini:
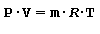
in cui:
P pressione [ bar ]
V volume occupato [ m3 ] m massa [kg]
R costante del gas che per l’aria è pari a 287.05 [ KJ/kg⋅K ]
T temperatura termodinamica in gradi Kelvin [ K ] ove ( 0 ºC corrisponde a 273,15 K )
Prima di valutare le varie trasformazioni che avvengono nei normali processi tecnologici si devono definire alcune terminologie:
Calore Si definisce Calore Q l’energia scambiata tra il sistema ed il suo contorno e solo nel momento in cui attraversa il sistema. Il calore non può essere immagazzinato e può essere solo convertito in qualche altra forma di energia solo dopo aver attraversato il contorno del sistema. La differenza di temperatura che è l’elemento essenziale che determina il trasferimento di calore è come stabilito dal II° principio della termodinamica il calore scambiato dai corpi o sistemi a temperatura più alta verso quelli a temperatura più bassa. Per convezione si assume che il trasferimento di calore sia positivo quando il calore viene aggiunto (entra) al sistema, mentre è negativo quando il calore viene rimosso (esce) dal sistema termodinamico.
Lavoro Si definisce Lavoro L l’energia scambiata tra il sistema e l’esterno ove la variabile che pilota lo scambio di energia non è la temperatura, come nel calore, ma una qualsiasi altra cosa diversa dalla temperatura. Per convenzione il lavoro è positivo quando è prodotto dal sistema (energia che esce dal sistema), mentre è negativo quando viene fatto sul sistema (energia che entra).
Entalpia Si definisce entalpia H oppure entalpia massica h la somma dell’energia interna del sistema u e del prodotto della pressione P per il volume massico V ed è quindi data da:
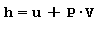
Entropia Si definisce entropia s una funzione di stato che misura la preferenza in natura per alcune trasformazioni ove la quantità di calore viene assorbita o ceduta in maniera reversibile ad una certa temperatura assoluta rispetto ad un determinato sistema di riferimento. Pertanto la variazione ideale di entropia riferita alla massa è data da:
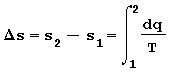
in cui:
dq è l’incremento infinitesimo del calore entrante (+) o uscente (-)
T è la temperatura assoluta del sistema. [ K ]
Capacita termica massica:
- Capacita termica massica a pressione costante Cp è la variazione di entalpia Δh per una variazione di temperatura ΔT in una trasformazione a pressione costante:

- Capacita termica massica a volume costante Cv è la variazione di energia interna Δu per una variazione di temperatura ΔT in una trasformazione a volume costante:
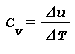
Per il I° principio della termodinamica le capacità termiche Cp e Cv sono legate alla costante del gas dalla relazione:
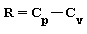
Trasformazione ISOCORA ossia a volume costante Somministrando del calore all’aria contenuta in un recipiente a pareti rigide la temperatura e la pressione aumentano. Il lavoro scambiato è nullo in quanto non c’è variazione di volume mentre la quantità di calore necessaria per passare dalla temperatura iniziale T1 alla temperatura finale T2 risulta:
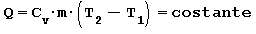
in cui:
Cv capacità termica massica a volume costante
m massa [ kg ]
L’aumento di pressione è legato all’aumento di temperatura dalla relazione seguente ricavabile dall’equazione di stato:
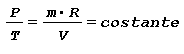
Tale relazione applicata alla variazione di temperatura tra T1 e T2 conduce a:
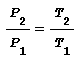
nota anche come legge di Amonton dalla quale si deduce che in una trasformazione a volume costante il rapporto tra le pressioni è uguale al rapporto tra le temperature.
Trasformazione ISOBARA ossia a pressione costante Se somministriamo del calore all’aria contenuta in un recipiente capace di mantenere la pressione costante la temperatura e il volume aumentano. La quantità di calore necessaria per passare dalla temperatura iniziale T1 alla temperatura finale T2 è uguale all’entalpia e risulta:
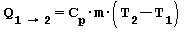
in cui:
Cp capacita termica massica a pressione costante
m massa [ kg ]
L’aumento di volume è legato all’aumento di temperatura dalla relazione seguente ricavabile dall’equazione di stato:
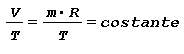
Tale relazione applicata alla variazione di temperatura tra T1 e T2 conduce a:
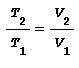
nota anche come legge di Charles dalla quale si deduce che in una trasformazione a pressione costante il rapporto tra i volumi e uguale al rapporto tra le temperature.
Trasformazione ISOTERMA ossia a temperatura costante Comprimendo dell’aria all’interno di un recipiente e sottraendo il calore generato in modo da mantenere la temperatura costante l’equazione di stato diventa:
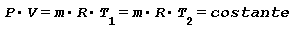
Tale relazione applicata alla variazione di volume diventa:
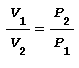
nota anche come legge di Boyle si deduce che il rapporto tra la variazione di pressione è inversamente proporzionale al rapporto tra la variazione di volume tramite un’equazione iperbolica equilatera. Il lavoro scambiato L1-2 durante questa trasformazione coincide con il calore Q1-2 e quindi risulta:
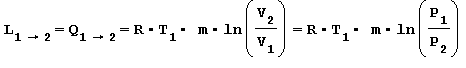
Trasformazione ADIABATICA ossia senza scambio di calore con l’esterno Trasformazione reversibile che avviene senza lo scambio termico con l’ambiente esterno ma solo con la variazione di lavoro e in base alla legge di Poisson risulta cosi espressa:
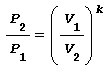
in cui:
k , che per l’aria risulta k=1,4, è il rapporto tra la capacità termica massica a pressione costante e la capacità termica massica a volume costante ovvero:
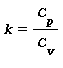
Altre equazioni utili equivalenti alla legge di Poisson sono:
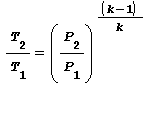
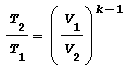
Trasformazione POLITROPICA ossia con scambio di calore con l’esterno Trasformazione reversibile ove si hanno variazione di temperatura, volume, pressione e scambio termico legati dalla seguente relazione:
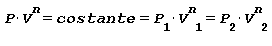
in cui:
n viene definito come esponente della politropica e assegnandoli un determinato valore si possono comprendere all’interno di questa equazione tutte le trasformazioni fino ad ora esaminate:
- n = 0 Trasformazione isobara
- n = 1 Trasformazione isoterma
- n = k Trasformazione adiabatica
- n = ∞ Trasformazione isocora

 Italian (IT)
Italian (IT)  English (UK)
English (UK)