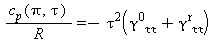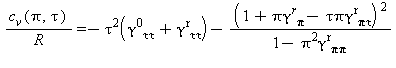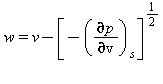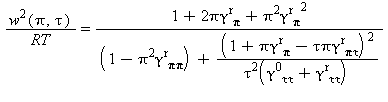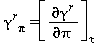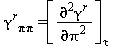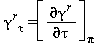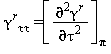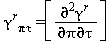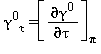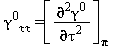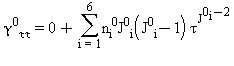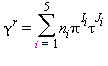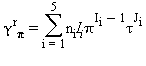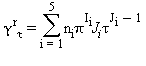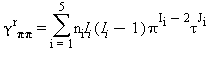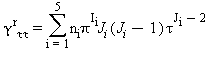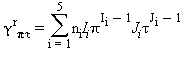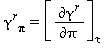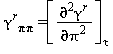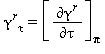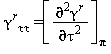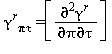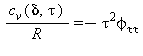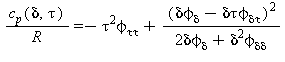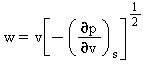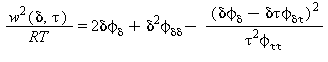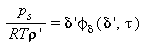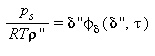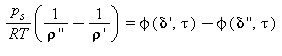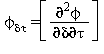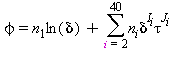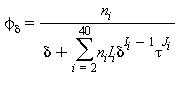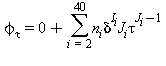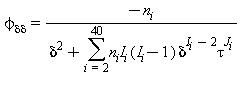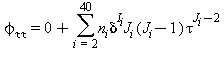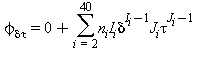Regione 5
- Pubblicato: Domenica, 27 Giugno 2010 06:34
- Scritto da Super User
- Visite: 8811
Equazioni di base
Le equazioni di base relative a questa regione, caratterizzata da vapore ad altissime temperature, coincidono con l’equazione fondamentale dell’energia libera di Gibbs g. Questa equazione espressa in forma adimensionale, γ=g/(RT), è divisa in due parti la prima si riferisce al gas ideale γ0 mentre la seconda alla parte residua γr :
![]() (32)
(32)
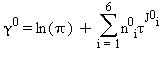 (33)
(33)
TABELLA 37
Valori dei coefficenti e degli esponenti della equazione adimensionale dell’energia libera di Gibbs relativi alla regione 5 come da eq. (33)
|
i
|
J0i
|
n0i
|
|
1
|
0
|
-0.131 799 836 742 01 x 102
|
|
2
|
1
|
0.685 408 416 344 34 x 101
|
|
3
|
-3
|
-0.248 051 489 334 66 x 10-1
|
|
4
|
-2
|
0.369 015 349 803 33
|
|
5
|
-1
|
-0.311 613 182 139 25 x 101
|
|
6
|
2
|
-0.329 616 265 389 17
|
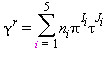 (34)
(34)
TABELLA 38
Valori dei coefficenti e degli esponenti della equazione della parte residua γr come da eq. (34)
|
i
|
Ii
|
Ji
|
ni
|
|
1
|
1
|
0
|
-0.125 631 835 895 92 x 10-3
|
|
2
|
1
|
1
|
0.217 746 787 145 71 x 10-2
|
|
3
|
1
|
3
|
-0.459 428 208 999 10 x 10-2
|
|
4
|
2
|
9
|
-0.397 248 283 595 69 x 10-5
|
|
5
|
3
|
3
|
0.129 192 282 897 84 x 10-6
|
Tutte le proprietà termodinamiche sono derivate dall’equazione (32) con la corretta combinazione della parte del gas-ideale γ0 eq.(33) e della parte residua γr eq.(34) relativi alla energia libera di Gibbs e relative derivate. Le proprietà più importanti incluso γ0 e γr con le relative derivate sono elencati nella tabella 39 mentre tutte le derivate richieste sono rispettivamente elencate nella tabella 40 e 41.
TABELLA 39
Relazioni tra le varie proprietà thermodinamiche sia la parte del gas-ideale γ0 sia la parte residua γr come da eq. (32);
|
Proprietà |
Relazione |
|
|
Volume specifico |
|
|
|
Energia specifica interna |
|
|
|
Entropia specifica |
|
|
|
Entalpia specifica |
|
|
|
Capacità termica massica a pressione costante |
|
|
|
Capacità termica massica a volume costante |
|
|
|
Velocità del suono |
|
|
|
|
||
TABELLA 40
Equazioni relative alla parte del gas-ideale γ0 come da eq. (33)
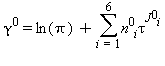 |
|
|
|
|
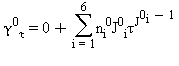 |
|
|
|
|
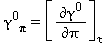 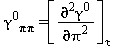 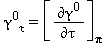 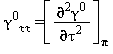 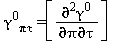 |
TABELLA 41
Equazioni relative alla parte residua γrcome da eq. (34)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
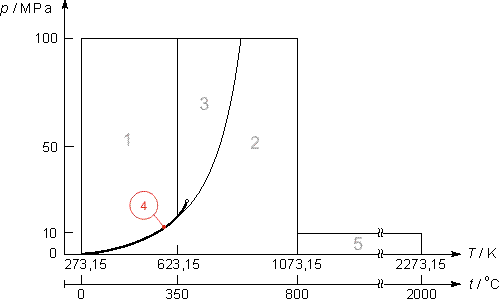
Intervallo di validità
L’equazione (32) è valida per il seguente intervallo di temperatura T e pressione p:
1073.15 K ≤ T ≤ 2273.15 K ; 0 < p ≤ 10 MPa
Inoltre le proprietà calcolate per la fase vapore ad altissime temperature ottenuti mediante l’eq.(32) sono valide solo per l’acqua completamente associata.
Test calcolo computer
La seguente tabella 42 contiene i valori di verifica relativi alla eq. (32).
TABELLA 42
Valori delle proprietà calcolati con l’eq. (32) in funzione di T e p
|
T = 1500K
p = 0,5 MPa
|
T = 1500K
p = 8 MPa
|
T = 2000K
p = 8 MPa
|
|
|
v (m³·kg-1)
|
0.138 455 354 x 101
|
0.865 156 616 x 10-1
|
0.115 743 146
|
|
h (kJ·kg-1)
|
0.521 976 332 x 104
|
0.520 609 634 x 104
|
0.658 380 291 x 104
|
|
u (kJ·kg-1)
|
0.452 748 654 x 104
|
0.451 397 105 x 104
|
0.565 785 774 x 104
|
|
s (kJ·kg-1·K-1)
|
0.965 408 431 x 101
|
0.836 546 724 x 101
|
0.915 671 044 x 101
|
|
cp (kJ·kg-1·K-1)
|
0.261 610 228 x 101
|
0.264 453 866 x 101
|
0.285 306 750 x 101
|
|
w (m·s-1)
|
0.917 071 933 x 10³
|
0.919 708 859 x 10³
|
0.105 435 806 x 104
|
- Categoria: IAPWS
Regione 4
- Pubblicato: Domenica, 27 Giugno 2010 06:32
- Scritto da Super User
- Visite: 8568
Equazioni fondamentali
L’equazione fondamentale che descrive la curva di saturazione, regione 4, che verrà usata successivamente per le equazioni di base e per le equazioni inverse è la seguente:
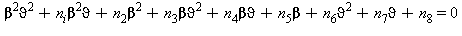 (29)
(29)
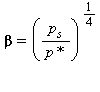 (29a)
(29a)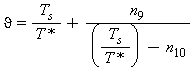 (29b)
(29b)Equazioni di base (calcolo pressione di saturazione ps)
L’equazione fondamentale (29) risolta in funzione della pressione di saturazione ps risulta:
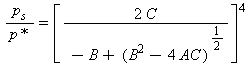 (30)
(30)
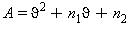
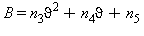
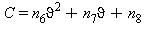
TABELLA 34
Valori dei coefficenti come da eq. (29) fino eq.(31)
|
i
|
ni
|
i
|
ni
|
|
1
|
0.116 705 214 527 67 x 104
|
6
|
0.149 151 086 135 30 x 102
|
|
2
|
-0.724 213 167 032 06 x 106
|
7
|
-0.482 326 573 615 91 x 104
|
|
3
|
-0.170 738 469 400 92 x 102
|
8
|
0.405 113 405 420 57 x 106
|
|
4
|
0.120 208 247 024 70 x 105
|
9
|
-0.238 555 575 678 49
|
|
5
|
-0.323 255 503 223 33 x 107
|
10
|
0.650 175 348 447 98 x 103
|
Intervallo di validità
Le equazioni che vanno dall’eq.(29) fino all’eq.(31) riproducono esattamente la relazione p-T; e il valore del triplo punto è in accordo con l’eq.(8) e con il punto normale di ebolizione (12) mentre il punto critico risulta in accordo con l’eq.(2) e (3). Inoltre l’eq.(30) è valida lungo tutta la curva che descrive il limite liquido-vapore a partire dal triplo punto, a cui corrisponde la temperatura Tt , fino al punto critico, a cui corrisponde una temperatura Tc , pertanto l’intervallo, in funzione di T, risulta:
273.15 K ≤ T ≤ 647.096 K
Test calcolo computer
La seguente tabella 35 contiene i valori di verifica relativi alla eq. (30).
TABELLA 35
Proprietà termodinamiche calcolati con l’eq. (30) in funzione di T
|
T (K)
|
ps (MPa)
|
|
300
|
0.353 658 941 x 10-2
|
|
500
|
0.263 889 776 x 10-1
|
|
600
|
0.123 443 146 x 102
|
Equazioni inverse (calcolo temperatura di saturazione Ts)
L’equazione fondamentale (29) risolta in funzione della temperatura di saturazione Ts risulta:
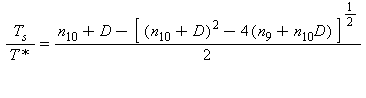 (31)
(31)
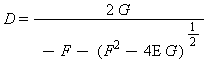
dove le variabili E, F, e G sono le seguenti:
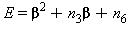
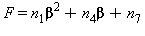
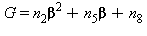
Intervallo di validità
L’equazione (31) ha lo stesso intervallo di validita dell’eq.(30) a cui corrisponde il seguente intervallo di pressione p:
611.213 Pa ≤ p ≤ 22.064 MPa
Test calcolo computer
La seguente tabella 36 contiene i valori di verifica relativi alla eq. (31).
TABELLA 36
Proprietà termodinamiche calcolati con l’eq. (31) in funzione di p
|
p (MPa)
|
Ts (K)
|
|
0.1
|
0.372 755 919 x 103
|
|
1
|
0.453 035 632 x 103
|
|
10
|
0.584 149 488 x 103
|
- Categoria: IAPWS
Subregione 2c
- Pubblicato: Domenica, 27 Giugno 2010 06:29
- Scritto da Super User
- Visite: 9339
In questa sezione sono presenti solo le equazioni inverse T(p,h) e T(p,s) relative alla sola subregione 2c. Per tutte le altre informazioni (eq. fondamentali, eq. di base, ecc.) consultare la regione 2.
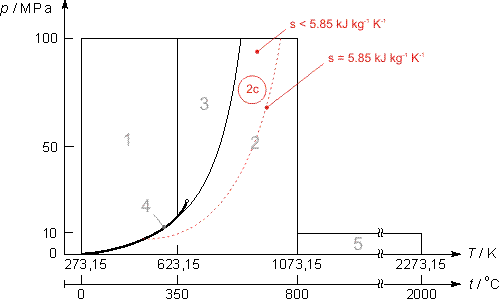
Equazione inversa T(p,h) subregione 2c
L’equazione inversa T(p,h) per la subregione 2c in forma adimensionale è la seguente:
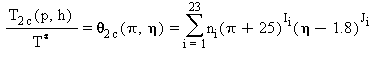 (24)
(24)
dove: θ=T/T*, p=p/p*, e η=h/h* con T*=1 K, p*=1 MPa, e h*=2000 kJ·kg-1.
I coefficenti ni e gli esponenti Ii e Ji si trovano nella seguente tabella 20c:
TABELLA 20c
Valori dei coefficenti e degli esponenti dell’equazione inversa T(p,h) relativa alla subregione 2c come da eq. (24)
|
i
|
Ii
|
Ji
|
ni
|
|
1
|
-7
|
0
|
-0.323 683 985 552 42 x 1013
|
|
2
|
-7
|
4
|
0.732 633 509 021 81 x 1013
|
|
3
|
-6
|
0
|
0.358 250 899 454 47 x 1012
|
|
4
|
-6
|
2
|
-0.583 401 318 515 90 x 1012
|
|
5
|
-5
|
0
|
-0.107 830 682 174 70 x 1011
|
|
6
|
-5
|
2
|
0.208 255 445 631 71 x 1011
|
|
7
|
-2
|
0
|
0.610 747 835 645 16 x 106
|
|
8
|
-2
|
1
|
0.859 777 225 355 80 x 106
|
|
9
|
-1
|
0
|
-0.257 457 236 041 70 x 105
|
|
10
|
-1
|
2
|
0.310 810 884 227 14 x 105
|
|
11
|
0
|
0
|
0.120 823 158 659 36 x 104
|
|
12
|
0
|
1
|
0.482 197 551 092 55 x 103
|
|
13
|
1
|
4
|
0.379 660 012 724 86 x 101
|
|
14
|
1
|
8
|
-0.108 429 848 800 77 x 102
|
|
15
|
2
|
4
|
-0.453 641 726 766 60 x 10-1
|
|
16
|
6
|
0
|
0.145 591 156 586 95 x 10-12
|
|
17
|
6
|
1
|
0.112 615 974 072 30 x 10-11
|
|
18
|
6
|
4
|
-0.178 049 822 406 86 x 10-10
|
|
19
|
6
|
10
|
0.123 245 796 908 32 x 10-6
|
|
20
|
6
|
12
|
-0.116 069 211 309 84 x 10-5
|
|
21
|
6
|
16
|
0.278 463 670 885 54 x 10-4
|
|
22
|
6
|
20
|
-0.592 700 384 741 76 x 10-3
|
|
23
|
6
|
22
|
0.129 185 829 918 78 x 10-2
|
Intervallo di validità
L’equazione (24) è valida solo per la subregione 2c e quindi sono escluse le regioni in fase vapore metastabile. La pressione piu bassa per l’eq.(24) ammonta a 611.153 Pa a cui corrisponde una temperatura di sublimazione pari a 273.15 K.
Tolleranza numerica
Per almeno 106 valori random calcolati in p ed in h la differenza ΔT tra le temperature calcolate con l’eq. (24) e l’eq. (15) devono soddisfare i seguenti criteri:
|ΔT|tol = 25 mK ; |ΔT|max = 23.7 mK ; ΔTrms = 10.4 mK
Test calcolo computer
La seguente tabella 22c contiene i valori di verifica relativi alla eq. (24).
TABELLA 22c
Valori delle temperature calcolati con l’eq. (24) in funzione di p e h
|
p (MPa)
|
h (kJ·kg-1)
|
T (K)
|
|
40
|
2700
|
0.743 056 411 x 103
|
|
60
|
2700
|
0.791 137 067 x 103
|
|
60
|
3200
|
0.882 756 860 x 103
|
Equazione inversa T(p,s) subregione 2c
L’equazione inversa T(p,s) per la subregione 2c in forma adimensionale è la seguente:
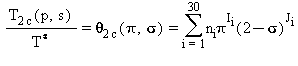 (27)
(27)
dove: θ=T/T*, p=p/p*, e σ=s/s* con T*=1 K, p*=1 MPa, e s*=2.9251 kJ·kg-1·K-1.
I coefficenti ni e gli esponenti Ii e Ji si trovano nella seguente tabella 21c:
TABELLA 21c
Valori dei coefficenti e degli esponenti dell’equazione inversa T(p,s) relativa alla regione 2c come da eq. (27)
|
i
|
Ii
|
Ji
|
ni
|
|
1
|
-2
|
0
|
0.909 685 010 053 65 x 103
|
|
2
|
-2
|
1
|
0.240 456 670 884 20 x 104
|
|
3
|
-1
|
0
|
-0.591 623 263 871 30 x 103
|
|
4
|
0
|
0
|
0.541 454 041 280 74 x 103
|
|
5
|
0
|
1
|
-0.270 983 084 111 92 x 103
|
|
6
|
0
|
2
|
0.979 765 250 979 26 x 103
|
|
7
|
0
|
3
|
-0.469 667 729 594 35 x 103
|
|
8
|
1
|
0
|
0.143 992 746 047 23 x 102
|
|
9
|
1
|
1
|
-0.191 042 042 304 29 x 102
|
|
10
|
1
|
3
|
0.532 991 671 119 71 x 101
|
|
11
|
1
|
4
|
-0.212 529 753 759 34 x 102
|
|
12
|
2
|
0
|
-0.311 473 344 137 60
|
|
13
|
2
|
1
|
0.603 348 408 946 23
|
|
14
|
2
|
2
|
-0.427 648 397 025 09 x 10-1
|
|
15
|
3
|
0
|
0.581 855 972 552 59 x 10-2
|
|
16
|
3
|
1
|
-0.145 970 082 847 53 x 10-1
|
|
17
|
3
|
5
|
0.566 311 756 310 27 x 10-2
|
|
18
|
4
|
0
|
-0.761 558 645 845 77 x 10-4
|
|
19
|
4
|
1
|
0.224 403 429 193 32 x 10-3
|
|
20
|
4
|
4
|
-0.125 610 950 134 13 x 10-4
|
|
21
|
5
|
0
|
0.633 231 326 609 34 x10-6
|
|
22
|
5
|
1
|
-0.205 419 896 753 75 x 10-5
|
|
23
|
5
|
2
|
0.364 053 703 900 82 x 10-7
|
|
24
|
6
|
0
|
-0.297 598 977 892 15 x 10-8
|
|
25
|
6
|
1
|
0.101 366 185 297 63 x 10-7
|
|
26
|
7
|
0
|
0.599 257 196 923 51 x 10-11
|
|
27
|
7
|
1
|
-0.206 778 701 051 64 x 10-10
|
|
28
|
7
|
3
|
-0.208 742 781 818 86 x 10-10
|
|
29
|
7
|
4
|
0.101 621 668 250 89 x 10-9
|
|
30
|
7
|
5
|
-0.164 298 282 813 47 x 10-9
|
Intervallo di validità
L’equazione (27) è valida solo per la subregione 2c e quindi sono escluse le regioni in fase vapore metastabile. La pressione piu bassa per l’eq.(27) ammonta a 611.153 Pa a cui corrisponde una temperatura di sublimazione pari a 273.15 K.
Tolleranza numerica
Per almeno 106 valori random calcolati in p ed in s la differenza ΔT tra le temperature calcolate con l’eq. (27) e l’eq. (15) devono soddisfare i seguenti criteri:
|ΔT|tol = 25 mK ; |ΔT|max = 19.0 mK ; ΔTrms = 8.3 mK
Test calcolo computer
La seguente tabella 23c contiene i valori di verifica relativi alla eq. (27).
TABELLA 23c
Valori delle temperature calcolati con l’eq. (27) in funzione di p e s
|
p (MPa)
|
s (kJ·kg-1·K-1)
|
T (K)
|
|
20
|
5.75
|
0.697 992 849 x 103
|
|
80
|
5.25
|
0.854 011 484 x 103
|
|
80
|
5.75
|
0.949 017 998 x 104
|
- Categoria: IAPWS
Regione 3
- Pubblicato: Domenica, 27 Giugno 2010 06:30
- Scritto da Super User
- Visite: 8999
Equazioni di base
Le equazioni di base relative a questa regione coincidono con l’equazione fondamentale dell’energia libera di Helmholtz f. Questa equazione espressa in forma adimensionale, Φ=f /(RT), si legge:
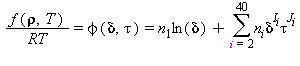 (28)
(28)
TABELLA 30
Valori dei coefficenti e degli esponenti della equazione adimensionale dell’energia libera di Helmholtz relativi alla regione 3 come da eq. (28)
|
i
|
I i
|
Ji
|
ni
|
|
1
|
0
|
0
|
0.106 580 700 285 13 x 101
|
|
2
|
0
|
0
|
-0.157 328 452 902 39 x 102
|
|
3
|
0
|
1
|
0.029 443 969 743 07 x 102
|
|
4
|
0
|
2
|
-0.768 677 078 787 16 x 101
|
|
5
|
0
|
7
|
0.261 859 477 879 54 x 101
|
|
6
|
0
|
10
|
-0.280 807 811 486 20 x 101
|
|
7
|
0
|
12
|
0.120 533 696 965 17 x 101
|
|
8
|
0
|
23
|
-0.845 668 128 125 02 x 10-2
|
|
9
|
1
|
2
|
-0.126 543 154 777 14 x 101
|
|
10
|
1
|
6
|
-0.115 244 078 066 81 x 101
|
|
11
|
1
|
15
|
0.885 210 439 843 18
|
|
12
|
1
|
17
|
-0.642 077 651 816 07
|
|
13
|
2
|
0
|
0.384 934 601 866 71
|
|
14
|
2
|
2
|
-0.852 147 088 242 06
|
|
15
|
2
|
6
|
0.489 722 815 418 77 x 101
|
|
16
|
2
|
7
|
-0.305 026 172 569 65 x 10-1
|
|
17
|
2
|
22
|
0.394 205 368 791 54 x 10-1
|
|
18
|
2
|
26
|
0.125 584 084 243 08
|
|
19
|
3
|
0
|
-0.279 993 296 987 10
|
|
20
|
3
|
2
|
0.138 997 995 694 60x 101
|
|
21
|
3
|
4
|
-0.201 899 150 235 70 x 101
|
|
22
|
3
|
16
|
-0.821 476 371 739 63 x 10-2
|
|
23
|
3
|
26
|
-0.475 960 357 349 23
|
|
24
|
4
|
0
|
0.439 840 744 735 00 x 10-1
|
|
25
|
4
|
2
|
-0.444 764 354 287 39
|
|
26
|
4
|
4
|
0.905 720 707 197 33
|
|
27
|
4
|
26
|
0.705 224 500 879 67
|
|
28
|
5
|
1
|
0.107 705 126 263 32
|
|
29
|
5
|
3
|
-0.329 136 232 589 54
|
|
30
|
5
|
26
|
-0.508 710 620 411 58
|
|
31
|
6
|
0
|
-0.221 754 008 730 96 x 10-1
|
|
32
|
6
|
2
|
0.942 607 516 650 92 x 10-1
|
|
33
|
6
|
26
|
0.164 362 784 479 61
|
|
34
|
7
|
2
|
-0.135 033 722 413 48 x 10-1
|
|
35
|
8
|
26
|
-0.148 343 453 524 72 x 10-1
|
|
36
|
9
|
2
|
0.579 229 536 280 84 x 10-3
|
|
37
|
9
|
26
|
0.323 089 047 037 11 x 10-2
|
|
38
|
10
|
0
|
0.809 648 029 962 15 x 10-4
|
|
39
|
10
|
1
|
-0.165 576 797 950 37 x 10-3
|
|
40
|
11
|
26
|
-0.449 238 990 618 15 x 10-4
|
Tutte le proprietà termodinamiche sono derivate dall’equazione (28) con la corretta combinazione degli indici relativi alla energia libera di Helmholtz e relative derivate. Le proprietà più importanti incluso F e relative derivate sono elencati nella tabella 31 mentre tutte le derivate relative all’energia libera di Helmholtz sono elencate nella tabella 32.
TABELLA 31
Relazioni tra le varie proprietà termodinamiche come da eq. (28)
|
Proprietà |
Relazione |
|
|
Pressione |
|
|
|
Energia specifica interna |
|
|
|
Entropia specifica |
|
|
|
Entalpia specifica |
|
|
|
Capacità termica massica a volume costante |
|
|
|
Capacità termica massica a pressione costante |
|
|
|
Velocità del suono |
|
|
|
Condizione di fase in equilibrio |
Legge di Maxwell |
|
|
|
||
TABELLA 32
Relazioni tra le varie proprietà termodinamiche come da eq. (28)
|
|
|
|
|
|
|
|
|
|
|
|
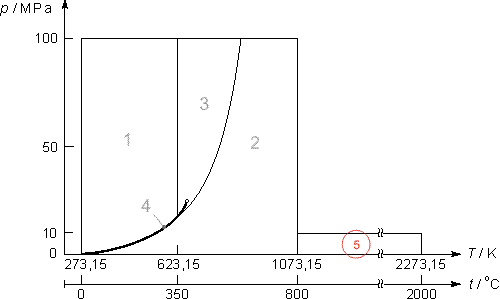
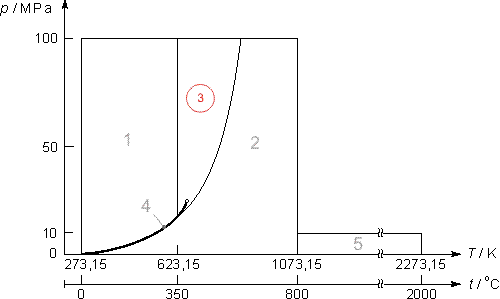
Intervallo di validità
L’equazione (28) è valida per i seguenti valori di temperatura T e pressione p:
623.15 K ≤ T ≤ T(p)eq.(6)
p(T)eq.(5) ≤ p ≤ 100 MPa
Test calcolo computer
La seguente tabella 33 contiene i valori di verifica relativi alla eq. (28).
TABELLA 33
Valori delle proprietà calcolati con l’eq. (28) in funzione di T e ρ
|
T = 650 K
ρ = 500 kg·m-3
|
T = 650 K
ρ = 200 kg·m -3
|
T = 750 K
ρ = 500 kg·m-3
|
|
|
p (Mpa)
|
0.255 837 018 x 10²
|
0.222 930 643 x 102
|
0.783 095 639 x 102
|
|
h (kJ·kg-1)
|
0.186 343 019 x 104
|
0.237 512 401 x 104
|
0.225 868 845 x 104
|
|
u (kJ kg-1)
|
0.181 226 279 x 104
|
0.226 365 868 x 104
|
0.210 206 932 x 104
|
|
s (kJ·kg-1·K-1)
|
0.405 427 273 x 101
|
0.485 438 792 x 101
|
0.446 971 906 x 101
|
|
cp (kJ·kg-1·K-1)
|
0.138 935 717 x 102
|
0.446 579 342 x 102
|
0.634 165 359 x 101
|
|
w (m·s-1)
|
0.502 005 554 x 103
|
0.383 444 594 x 103
|
0.760 696 041 x 103
|
- Categoria: IAPWS
Subregione 2a
- Pubblicato: Domenica, 27 Giugno 2010 06:27
- Scritto da Super User
- Visite: 8788
In questa sezione sono presenti solo le equazioni inverse T(p,h) e T(p,s) relative alla sola subregione 2a. Per tutte le altre informazioni (eq. fondamentali,eq. di base, ecc.) consultare la regione 2.
Equazione inversa T(p,h) subregione 2a
L’equazione inversa T(p,h) per la subregione 2a in forma adimensionale è la seguente:
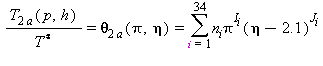 (22)
(22)
dove: θ=T/T*, p=p/p*, e η=h/h* con T*=1 K, p*=1 MPa, e h*=2000 kJ·kg-1.
I coefficenti ni e gli esponenti Ii e Ji si trovano nella seguente tabella 20a:
TABELLA 20a
Valori dei coefficenti e degli esponenti dell’equazione inversa T(p,h) relativa alla subregione 2a come da eq. (22)
|
i
|
Ii
|
Ji
|
ni
|
|
1
|
0
|
0
|
0.180 989 523 182 88 x 104
|
|
2
|
0
|
1
|
0.849 516 544 955 35 x 103
|
|
3
|
0
|
2
|
-0.107 817 480 918 26 x 103
|
|
4
|
0
|
3
|
0.331 536 548 012 63 x 102
|
|
5
|
0
|
7
|
-0.742 302 167 902 48 x 101
|
|
6
|
0
|
20
|
0.117 650 487 243 56 x 102
|
|
7
|
1
|
0
|
0.184 457 493 557 90 x 101
|
|
8
|
1
|
1
|
-0.417 927 005 496 24 x 101
|
|
9
|
1
|
2
|
0.624 781 969 358 12 x 101
|
|
10
|
1
|
3
|
-0.173 445 631 081 14 x 102
|
|
11
|
1
|
7
|
-0.200 581 768 620 96 x 103
|
|
12
|
1
|
9
|
0.271 960 654 737 96 x 103
|
|
13
|
1
|
11
|
-0.455 113 182 858 18 x 103
|
|
14
|
1
|
18
|
0.309 196 886 047 55 x 104
|
|
15
|
1
|
44
|
0.252 266 403 578 72 x 106
|
|
16
|
2
|
0
|
-0.617 074 228 683 39 x 10-2
|
|
17
|
2
|
2
|
-0.310 780 466 295 83
|
|
18
|
2
|
7
|
0.116 708 730 771 07 x 102
|
|
19
|
2
|
36
|
0.128 127 984 040 46 x 109
|
|
20
|
2
|
38
|
-0.985 549 096 23 76 x 109
|
|
21
|
2
|
40
|
0.282 245 469 730 02 x 1010
|
|
22
|
2
|
42
|
-0.359 489 714 107 03 x 1010
|
|
23
|
2
|
44
|
0.172 273 499 131 97 x 1010
|
|
24
|
3
|
24
|
-0.135 513 342 407 75 x 105
|
|
25
|
3
|
44
|
0.128 487 346 646 50 x 108
|
|
26
|
4
|
12
|
0.138 657 242 832 26 x 101
|
|
27
|
4
|
32
|
0.235 988 325 565 14 x 106
|
|
28
|
4
|
44
|
-0.131 052 365 450 54 x 108
|
|
29
|
5
|
32
|
0.739 998 354 747 66 x 104
|
|
30
|
5
|
36
|
-0.551 966 970 300 60 x 106
|
|
31
|
5
|
42
|
0.371 540 859 962 33 x 107
|
|
32
|
6
|
34
|
0.191 277 292 396 60 x 105
|
|
33
|
6
|
44
|
-0.415 351 648 356 34 x 106
|
|
34
|
7
|
28
|
-0.624 598 551 925 07 x 102
|
Intervallo di validità
L’equazione (22) è valida solo per la subregione 2a e quindi sono escluse le regioni in fase vapore metastabile. La pressione piu bassa per l’eq.(22) ammonta a 611.153 Pa a cui corrisponde una temperatura di sublimazione pari a 273.15 K.
Tolleranza numerica
Per almeno 106 valori random calcolati in p ed in h la differenza ΔT tra le temperature calcolate con l’eq. (22) e l’eq. (15) devono soddisfare i seguenti criteri:
|ΔT|tol = 10 mK ; |ΔT|max = 9.3 mK ; ΔTrms = 2.9 mK
Test calcolo computer
La seguente tabella 22a contiene i valori di verifica relativi alla eq. (22).
TABELLA 22a
Valori delle temperature calcolati con l’eq. (22) in funzione di p e h
|
p (MPa)
|
h (kJ·kg-1)
|
T (K)
|
|
0.001
|
3000
|
0.534 433 241 x 103
|
|
3
|
3000
|
0.575 373 370 x 103
|
|
3
|
4000
|
0.101 077 577 x 104
|
Equazione inversa T(p,s) subregione 2a
L’equazione inversa T(p,s) per la subregione 2a in forma adimensionale è la seguente:
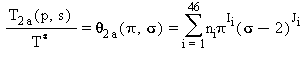 (25)
(25)
dove: θ=T/T*, p=p/p*, e σ=s/s* con T*=1 K, p*=1 MPa, e s*=2 kJ·kg-1·K-1.
I coefficenti ni e gli esponenti Ii e Ji si trovano nella seguente tabella 21a:
TABELLA 21a
Valori dei coefficenti e degli esponenti dell’equazione inversa T(p,s) relativa alla regione 2a come da eq. (25)
|
I
|
Ii
|
Ji
|
ni
|
|
1
|
-1,5
|
-24
|
-0,392 359 838 619 84 x 106
|
|
2
|
-1,5
|
-23
|
0,515 265 738 272 70 x 106
|
|
3
|
-1,5
|
-19
|
0,404 824 431 610 48 x 105
|
|
4
|
-1,5
|
-13
|
-0,321 937 909 239 02 x 103
|
|
5
|
-1,5
|
-11
|
0,969 614 242 186 94 x 102
|
|
6
|
-1,5
|
-10
|
-0,228 678 463 717 73 x 102
|
|
7
|
-1,25
|
-19
|
-0,449 429 141 243 57 x 106
|
|
8
|
-1,25
|
-15
|
-0,501 183 360 201 66 x 104
|
|
9
|
-1,25
|
-6
|
0,356 844 635 600 15
|
|
10
|
-1,0
|
-26
|
0,442 353 358 481 90 x 105
|
|
11
|
-1,0
|
-21
|
-0,136 733 888 117 08 x 105
|
|
12
|
-1,0
|
-17
|
0,421 632 602 078 64 x 106
|
|
13
|
-1,0
|
-16
|
0,225 169 258 374 75 x 105
|
|
14
|
-1,0
|
-9
|
0,474 421 448 656 46 x 103
|
|
15
|
-1,0
|
-8
|
-0,149 311 307 976 47 x 103
|
|
16
|
-0,75
|
-15
|
-0,197 811 263 204 52 x 106
|
|
17
|
-0,75
|
-14
|
-0,235 543 994 707 60 x 105
|
|
18
|
-0,5
|
-26
|
-0,190 706 163 020 76 x 105
|
|
19
|
-0,5
|
-13
|
0,553 756 698 831 64 x 105
|
|
20
|
-0,5
|
-9
|
0,382 936 914 373 63 x 104
|
|
21
|
-0,5
|
-7
|
-0,603 918 605 805 67 x 103
|
|
22
|
-0,25
|
-27
|
0,193 631 026 203 31 x 104
|
|
23
|
-0,25
|
-25
|
0,426 606 436 986 10 x 104
|
|
24
|
-0,25
|
-11
|
-0,597 806 388 727 18 x 104
|
|
25
|
-0,25
|
-6
|
-0,704 014 639 268 62 x 103
|
|
26
|
0,25
|
1
|
0,338 367 841 075 53 x 103
|
|
27
|
0,25
|
4
|
0,208 627 866 351 87 x 102
|
|
28
|
0,25
|
8
|
0,338 341 726 561 96 x 10-1
|
|
29
|
0,25
|
11
|
-0,431 244 284 148 93 x 10-4
|
|
30
|
0,50
|
0
|
0,166 537 913 564 12 x 103
|
|
31
|
0,5
|
1
|
-0,139 862 920 558 98 x 103
|
|
32
|
0,5
|
5
|
-0,788 495 479 998 72
|
|
33
|
0,5
|
6
|
0,721 324 117 538 72 x 10-1
|
|
34
|
0,5
|
10
|
-0,597 548 393 982 83 x 10-2
|
|
35
|
0,5
|
14
|
-0,121 413 589 539 04 x 10-4
|
|
36
|
0,5
|
16
|
0,232 270 967 338 71 x 10-6
|
|
37
|
0,75
|
0
|
-0,105 384 635 661 94 x 102
|
|
38
|
0,75
|
4
|
0,207 189 254 965 02 x 101
|
|
39
|
0,75
|
9
|
-0,721 931 552 604 27 x 10-1
|
|
40
|
0,75
|
17
|
0,207 498 870 811 20 x 10-6
|
|
41
|
1,0
|
7
|
-0,183 406 579 113 79 x 10-1
|
|
42
|
1,0
|
18
|
0,290 362 723 486 96 x 10-6
|
|
43
|
1,25
|
3
|
0,210 375 278 936 19
|
|
44
|
1,25
|
15
|
0,256 812 397 299 99 x 10-3
|
|
45
|
1,5
|
5
|
-0,127 990 029 337 81 x 10-1
|
|
46
|
1,5
|
18
|
-0,821 981 026 520 18 x 10-5
|
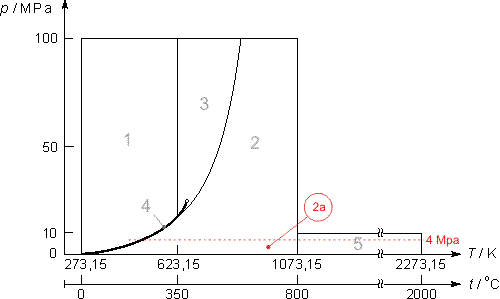
Intervallo di validità
L’equazione (25) è valida solo per la subregione 2a e quindi sono escluse le regioni in fase vapore metastabile. La pressione piu bassa per l’eq.(25) ammonta a 611.153 Pa a cui corrisponde una temperatura di sublimazione pari a 273.15 K.
Tolleranza numerica
Per almeno 106 valori random calcolati in p ed in s la differenza ΔT tra le temperature calcolate con l’eq. (25) e l’eq. (15) devono soddisfare i seguenti criteri:
|ΔT|tol = 10 mK ; |ΔT|max = 8.8 mK ; ΔTrms = 1.2 mK
Test calcolo computer
La seguente tabella 23a contiene i valori di verifica relativi alla eq. (25).
TABELLA 23a
Valori delle temperature calcolati con l’eq. (25) in funzione di p e s
|
p (MPa)
|
s (kJ·kg-1·K-1)
|
T (K)
|
|
0.1
|
7.5
|
0.399 517 097 x 103
|
|
0.1
|
8
|
0.514 127 081 x 103
|
|
2.5
|
8
|
0.103 984 917 x 104
|
- Categoria: IAPWS

 Italian (IT)
Italian (IT)  English (UK)
English (UK)